Cabdullahi
IB Legend
- Messages
- 5,610
- Reaction score
- 1,308
- Gender
- Male
- Religion
- Islam
Because i cant be arsed to revise for the exam tomorrow ive come up with an idea that could benefit me and also you guys 
This is mesh analysis
A mesh is a closed loop(starting at a node and returning along that same node without passing through an intermediary node
Basically mesh analysis is a powerful way to calculate and analysis circuits
ok first and foremost we need a circuit to work from
and here it is sorry about the quality of the drawing Ive used paint
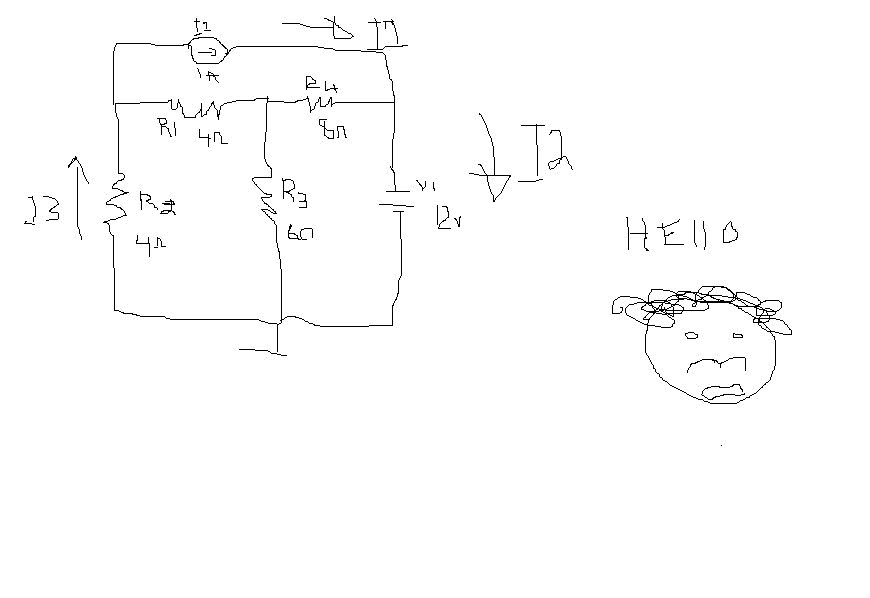
to clarify the values of the components:
R1 = 4 Ohms
R2 = 4 Ohms
R3 = 6 Ohms
R4 = 8 Ohms
V = 12 volts
I = 1 Ampere
basically we will divide up the circuit into three loops
loop one is the box containing the voltage source and the 2 resisters
that's V12 , R3 and R4
so using the algebraic formula
we put all the values together
so ......v12=R3(I2-I3) - R4(12-13)
what we want to find is the unknown value of the current we've got the resistance and the voltage
v12=R3(I2-I3) - R4(12-13)
^
^
^
we rewrite it but this time with the values in
R3 = 6 Ohms
R4 = 8 Ohms
V = 12 volts
I1,I2,I3...Unknown
V12=R2(I2-I3) - R4
we then move everything we know to the right and everything we dont know to the left
PUT THE VALUES IN and this is what you get
v12 = 6(I2)-6(I3) - 8(12) - 8
we then move everything we know to the right and everything we dont know to the left
so 20 = 14I2 - 6 I3
Thats the equation complete for loop 1
now loop 2
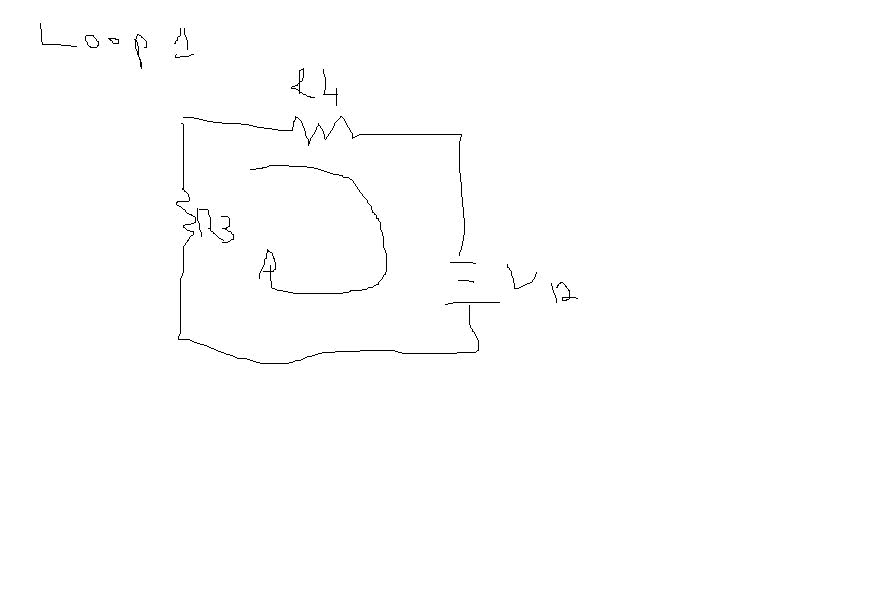
the values
R1 = 4 Ohms
R2 = 4 Ohms
R3 = 6 Ohms
because there isn't any source we take it as 0
0=R2(I3) + R1 (I3-I1) + R3 (I3-I2)
PUT THE VALUES IN and we get
0=4(I3) + 4(I3) - 4 + 6(I3) - 6(I2)
the left over 4 from I3 will be treated like a source because we cannot have 0 as a value it wouldn't work
move all the known values to the right and the unknown to the left
you get
4 = 14(13) - 6(I2)........ loop 2
now this bit is where i always struggle because my maths is pants:rollseyes .....to find the current through R2 we simply use simultaneous equation to derive the current through resistor 3
20 = 14 I2 - 6 I3
4 = - 6 I2 - 14 I2
----------------
14/6 gives you 2.3333333333
you multiply the bottom to get it to look like the top
4 = - 6 I2 - 14 I2 >>>>>will become this >>>>>9.333333332 = 14 - 32.66666666
20 = 14 I2 - 6 I3
9.333333332 = 14 I2 - 32.66666666I3
canceled
20 = - 6 I3
9.333333332 = - 32.66666666I3
---------------------------------
10.7 = 26.7
divide 10.7 by 26.7 to get I3
10.7/26.7=0.4007ampere
I3=0.4007
and that's mesh analysis
other members who are doing the same or similar can you guys assist me or the those who are good at maths maybe you guys can help me with the simultaneous bit
This is mesh analysis
A mesh is a closed loop(starting at a node and returning along that same node without passing through an intermediary node
Basically mesh analysis is a powerful way to calculate and analysis circuits
ok first and foremost we need a circuit to work from
and here it is sorry about the quality of the drawing Ive used paint

to clarify the values of the components:
R1 = 4 Ohms
R2 = 4 Ohms
R3 = 6 Ohms
R4 = 8 Ohms
V = 12 volts
I = 1 Ampere
basically we will divide up the circuit into three loops
loop one is the box containing the voltage source and the 2 resisters
that's V12 , R3 and R4
so using the algebraic formula
we put all the values together
so ......v12=R3(I2-I3) - R4(12-13)
what we want to find is the unknown value of the current we've got the resistance and the voltage
v12=R3(I2-I3) - R4(12-13)
^
^
^
we rewrite it but this time with the values in
R3 = 6 Ohms
R4 = 8 Ohms
V = 12 volts
I1,I2,I3...Unknown
V12=R2(I2-I3) - R4
we then move everything we know to the right and everything we dont know to the left
PUT THE VALUES IN and this is what you get
v12 = 6(I2)-6(I3) - 8(12) - 8
we then move everything we know to the right and everything we dont know to the left
so 20 = 14I2 - 6 I3
Thats the equation complete for loop 1
now loop 2

the values
R1 = 4 Ohms
R2 = 4 Ohms
R3 = 6 Ohms
because there isn't any source we take it as 0
0=R2(I3) + R1 (I3-I1) + R3 (I3-I2)
PUT THE VALUES IN and we get
0=4(I3) + 4(I3) - 4 + 6(I3) - 6(I2)
the left over 4 from I3 will be treated like a source because we cannot have 0 as a value it wouldn't work
move all the known values to the right and the unknown to the left
you get
4 = 14(13) - 6(I2)........ loop 2
now this bit is where i always struggle because my maths is pants:rollseyes .....to find the current through R2 we simply use simultaneous equation to derive the current through resistor 3
20 = 14 I2 - 6 I3
4 = - 6 I2 - 14 I2
----------------
14/6 gives you 2.3333333333
you multiply the bottom to get it to look like the top
4 = - 6 I2 - 14 I2 >>>>>will become this >>>>>9.333333332 = 14 - 32.66666666
20 = 14 I2 - 6 I3
9.333333332 = 14 I2 - 32.66666666I3
canceled
20 = - 6 I3
9.333333332 = - 32.66666666I3
---------------------------------
10.7 = 26.7
divide 10.7 by 26.7 to get I3
10.7/26.7=0.4007ampere
I3=0.4007
and that's mesh analysis
other members who are doing the same or similar can you guys assist me or the those who are good at maths maybe you guys can help me with the simultaneous bit
