Abdul Fattah
a.k.a. steve
- Messages
- 1,931
- Reaction score
- 450
- Gender
- Male
- Religion
- Islam
Hi, in reference to a recent thread, I thought to calculate the chance of cousins having a child with a genetic defect based on the percentage of dormant disabilities within the populations. However I apparently made some mistakes, cause the results are nonsensical (ei: negative probability for a percentage of 100%)
Definitions:
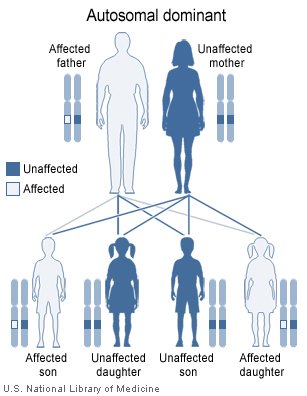
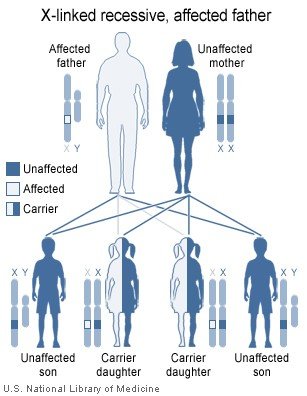
*People without genetic disability: (AA)
*People with genetic disability: (BB)
*Percentage of people with dormant trait (AB) or (BA): x
Objective:
* Find function f(x) that gives the percentage of two cousins having a child with trait (BB)
* Find function g(x) that gives the percentage of two unrelated people having a child with trait (BB)
* Compare which of the two cases has the highest risk
Note1: In laws should be considered to have a chance of x/100 of having (AB)
Note2: The chance of people of the first generations having (BB) is not added, we assume that in such cases there will be no further marriages and children from that generation.
Calculating:
First generation:
* The chance that a person has (AB):
x/100
* The chance that a person doesn't has (AB):
1-(x/100) = (100/100)-(x/100) = (100-x)/100
* Scenario p1; the chance that both partners have (AB):
(x/100)^2 = x^2/10000
* Scenario p2; the chance that neither partner has (AB):
[(100-x)/100]^2 = (100-x)^2/10000
* Scenario p3; the chance that one of the two partners has (AB):
2(x/100)[(100-x)/100] = (100x-x^2)/5000
Second generation:
* Chance that a child of 2nd gen has (AB): (p1/2 + p2*0 + p3/4)/4
[(x^2/10000)/2 + 0 + ((100x-x^2)/5000)/4]/4 =
[(x^2)/20000 + (100x-x^2)/20000]/4 = (100x^3-x^4)/80000
* Chance that a child of sec gen doesn't have (AB): 1-[(p1/2 + p2*0 + p3/4)/3]
1 -[(100x^3-x^4)/80000] =
(80000-100x^3-x^4)/80000
* Chance that a partner of the 2nd gen has (AB)
x/100
* Chance that a partner of the 2nd gen doesn't have (AB)
(100-x)/100
* Scenario q1; the chance that both children of 2nd gen and their partners have (AB):
[[(100x^3-x^4)/80000]^2]*[(x/100)^2] =
[(100x^3-x^4)^2/(64*10^8)]*[x^2/10000] =
(10^4x^6-200x^7+x^4)(x^2)/(46*10^12) =
(10^4x^8-200x^9+x^6)/(46*10^12)
* Scenario q2; the chance that both children of 2nd gen and one of their partners have (AB):
[[(100x^3-x^4)/80000]^2]*[(100x-x^2)/5000] =
[(100x^3-x^4)^2/(64*10^8)]*[(100x-x^2)/5000] =
(10^4x^6-200x^7+x^4)(100x-x^2)/(64*10^12) =
(100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9)/(64*10^12)
* Scenario q3; the chance that both children of 2nd gen but none of their partners have (AB):
[[(100x^3-x^4)/60000]^2]*[(100-x)^2/10000] =
[(100x^3-x^4)^2/(64*10^8)]*[(100-x)^2/10000] =
(10^4x^6-200x^7+x^4)(10^4 -200x +x^2)/(64*10^12) =
(10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7+ 4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6)/(64*10^12)
* Scenario q4; the chance that neither of the children of 2nd gen but both partners have (AB):
[[1-[(100x^3-x^4)/80000]]^2]*[(x/100)^2] =
[(80000-100x^3-x^4)^2/(64*10^8)]*[x^2/10000] =
(64*10^8 -16*10^6x^3 -16*10^4x^4 +10^4x^6 +200x^7 +x^8)(x^2)/(64*10^12) =
(64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10)/(64*10^12)
* Scenario q5; the chance that neither of the children of 2nd gen but one partners has (AB):
[[1-[(100x^3-x^4)/80000]]^2]*[(100x-x^2)/5000] =
[(80000-100x^3-x^4)^2/(64*10^8)]*[(100x-x^2)/5000] =
2(64*10^8 -16*10^6x^3 -16*10^4x^4 +10^4x^6 +200x^7 +x^8)(100x-x^2)/(32*10^12) =
4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10)/(64*10^12)
* Scenario q6; the chance that nor the children of 2nd gen nor their partners have (AB):
(moot issue)
* Scenario q7; the chance that one of the children of second gen and their partners have (AB):
2[(100x^3-x^4)/80000][(60000-100x^3-x^4)/80000]*[(x/100)^2] =
2[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[x^2/10000] =
2[(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(x^2)/(64*10^12) =
2[(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10)/(64*10^12)
* Scenario q8; the chance that one of the children of second gen but neither partners have (AB):
2[(100x^3-x^4)/80000][(80000-100x^3-x^4)/80000]*[(100-x)^2/10000] =
2[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[(100-x)^2/10000] =
2(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(10^4 -200x +x^2)/(64*10^12) =
2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10)/(64*10^12)
* Scenario q9; the chance that one of the children of second gen and only his partners have (AB):
[(100x^3-x^4)/80000][(80000-100x^3-x^4)/80000]*[(100x-x^2)/5000] =
[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[(100x-x^2)/5000] =
(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(100x-x^2)/(32*10^12) =
2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
* Scenario q10; the chance that one of the children of second gen and only the partner of the other child of the 2nd gen have (AB):
[(100x^3-x^4)/80000][(80000-100x^3-x^4)/80000]*[(100x-x^2)/5000] =
[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[(100x-x^2)/5000] =
(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(100x-x^2)/(32*10^12) =
2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
Third generation:
* Chance that a child from the 3th gen has (AB):
[q1/2 + (q2/2 + q2/4)/2 + q3/4 + q4/4 + (q5*0 + q5/4)/2 + q6*0 + (q7/2 + q7/4)/2 + (q8*0 +q8/4)/2 + (q9*0 + q9/2)/2 + q10/4]/10 =
(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)/10
* Scenario r; the chance that both cousins from the 3th gen have (AB):
[(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)/10]^2
(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)^2/100
Fourth generation:
* Chance that the child from our two cousins is born with a genetic defect (BB):
f(x) = r/4
f(x) = [(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)^2/100]/4
f(x) = (4q1/8 + 3q2/8 + 2q3/8 + 2q4/8 + q5/8 + 3q7/8 + q8/8 + 2q9/8 + 2q10/8)^2/400
f(x) = [(4q1 +3q2 +2q3 +2q4 +q5 +3q7 +q8 +2q9 +2q10)/8]^2/400
f(x) = (4q1 +3q2 +2q3 +2q4 +q5 +3q7 +q8 +2q9 +2q10)^2/256*10^2
If we now fill in the values:
q1 = (10^4x^8-200x^9+x^6)/(64*10^12)
q2 = (100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9)/(64*10^12)
q3 = (10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7+ 4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6)/(64*10^12)
q4 = (64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10)/(64*10^12)
q5 = 4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10)/(64*10^12)
q7 = 2[(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10)/(64*10^12)
q8 = 2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10)/(64*10^12)
q9 = 2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
q10 = 2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
We get:
f(x) = [4(10^4x^8-200x^9+x^6)/(64*10^12) +3(100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9)/(64*10^12) +2(10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7+ 4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6)/(64*10^12) +2(64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10)/(64*10^12) +4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10)/(64*10^12) +6(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10)/(64*10^12) +2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10)/(64*10^12) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)]^2/256*10^2
Adding up the fractions:
f(x) = [[4(10^4x^8-200x^9+x^6) +3(100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9) +2(10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7 +4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6) +2(64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10) +4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10) +6(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10) +2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)]^2/(64*10^12)^2]/256*10^2
Working out the numberator:
f(x) =[(4*10^4x^8-8*10^2x^9+4x^6 +3*10^2x^5 -3x^6 +3*10^6x^7 -9*10^4x^8 +6*10^2x^9 +2*10^8x^6 -4*10^6x^7 +2*10^4x^4 -4*10^6x^7 +8*10^4x^8 -400x^5 +2*10^4x^8 -400x^9 +2x^6 +128*10^8x^2 -32*10^6x^5 -32*10^4x^6 +2*10^4x^8 +400x^9 +2x^10 +256*10^10x -256*10^8x^2 -64*10^8x^4 +64*10^4x^6 +4*10^6x^7 +4*10^4x^8 -400x^9 -4x^10 +48*10^6x^5 -48*10^4x^6 -6*10^4x^8 +6x^10 +16*10^10x^3 -32*10^8x^4 +32*10^6x^5 -20016*10^4x^6 +2*10^6x^7 -2*10^2x^9 +2x^10 +32*10^8x^4 -64*10^6x^5 +32*10^4x^6 -4*10^6x^7 +4*10^4x^8 +4*10^2x^9 -4x^10 +32*10^8x^4 -64*10^6x^5 +32*10^4x^6 -4*10^6x^7 +4*10^4x^8 +4*10^2x^9 -4x^10)^2/(4.096*10^27)]/256*10^2
Adding up:
f(x) = (+256*10^10x -128*10^8x^2 +16*10^10x^3 -320002*10^4x^4 -800001*10^2x^5 +320003x^6 -7*10^6x^7 +13*10^4x^8 -2x^10)^2/(1.048576*10^32)
* The chance of two unrelated people having a child with trait (BB)
g(x) = [(x/100)^2]/4
g(x) = x^2/40000
Definitions:
*People without genetic disability: (AA)
*People with genetic disability: (BB)
*Percentage of people with dormant trait (AB) or (BA): x
Objective:
* Find function f(x) that gives the percentage of two cousins having a child with trait (BB)
* Find function g(x) that gives the percentage of two unrelated people having a child with trait (BB)
* Compare which of the two cases has the highest risk
Note1: In laws should be considered to have a chance of x/100 of having (AB)
Note2: The chance of people of the first generations having (BB) is not added, we assume that in such cases there will be no further marriages and children from that generation.
Calculating:
First generation:
* The chance that a person has (AB):
x/100
* The chance that a person doesn't has (AB):
1-(x/100) = (100/100)-(x/100) = (100-x)/100
* Scenario p1; the chance that both partners have (AB):
(x/100)^2 = x^2/10000
* Scenario p2; the chance that neither partner has (AB):
[(100-x)/100]^2 = (100-x)^2/10000
* Scenario p3; the chance that one of the two partners has (AB):
2(x/100)[(100-x)/100] = (100x-x^2)/5000
Second generation:
* Chance that a child of 2nd gen has (AB): (p1/2 + p2*0 + p3/4)/4
[(x^2/10000)/2 + 0 + ((100x-x^2)/5000)/4]/4 =
[(x^2)/20000 + (100x-x^2)/20000]/4 = (100x^3-x^4)/80000
* Chance that a child of sec gen doesn't have (AB): 1-[(p1/2 + p2*0 + p3/4)/3]
1 -[(100x^3-x^4)/80000] =
(80000-100x^3-x^4)/80000
* Chance that a partner of the 2nd gen has (AB)
x/100
* Chance that a partner of the 2nd gen doesn't have (AB)
(100-x)/100
* Scenario q1; the chance that both children of 2nd gen and their partners have (AB):
[[(100x^3-x^4)/80000]^2]*[(x/100)^2] =
[(100x^3-x^4)^2/(64*10^8)]*[x^2/10000] =
(10^4x^6-200x^7+x^4)(x^2)/(46*10^12) =
(10^4x^8-200x^9+x^6)/(46*10^12)
* Scenario q2; the chance that both children of 2nd gen and one of their partners have (AB):
[[(100x^3-x^4)/80000]^2]*[(100x-x^2)/5000] =
[(100x^3-x^4)^2/(64*10^8)]*[(100x-x^2)/5000] =
(10^4x^6-200x^7+x^4)(100x-x^2)/(64*10^12) =
(100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9)/(64*10^12)
* Scenario q3; the chance that both children of 2nd gen but none of their partners have (AB):
[[(100x^3-x^4)/60000]^2]*[(100-x)^2/10000] =
[(100x^3-x^4)^2/(64*10^8)]*[(100-x)^2/10000] =
(10^4x^6-200x^7+x^4)(10^4 -200x +x^2)/(64*10^12) =
(10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7+ 4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6)/(64*10^12)
* Scenario q4; the chance that neither of the children of 2nd gen but both partners have (AB):
[[1-[(100x^3-x^4)/80000]]^2]*[(x/100)^2] =
[(80000-100x^3-x^4)^2/(64*10^8)]*[x^2/10000] =
(64*10^8 -16*10^6x^3 -16*10^4x^4 +10^4x^6 +200x^7 +x^8)(x^2)/(64*10^12) =
(64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10)/(64*10^12)
* Scenario q5; the chance that neither of the children of 2nd gen but one partners has (AB):
[[1-[(100x^3-x^4)/80000]]^2]*[(100x-x^2)/5000] =
[(80000-100x^3-x^4)^2/(64*10^8)]*[(100x-x^2)/5000] =
2(64*10^8 -16*10^6x^3 -16*10^4x^4 +10^4x^6 +200x^7 +x^8)(100x-x^2)/(32*10^12) =
4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10)/(64*10^12)
* Scenario q6; the chance that nor the children of 2nd gen nor their partners have (AB):
(moot issue)
* Scenario q7; the chance that one of the children of second gen and their partners have (AB):
2[(100x^3-x^4)/80000][(60000-100x^3-x^4)/80000]*[(x/100)^2] =
2[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[x^2/10000] =
2[(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(x^2)/(64*10^12) =
2[(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10)/(64*10^12)
* Scenario q8; the chance that one of the children of second gen but neither partners have (AB):
2[(100x^3-x^4)/80000][(80000-100x^3-x^4)/80000]*[(100-x)^2/10000] =
2[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[(100-x)^2/10000] =
2(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(10^4 -200x +x^2)/(64*10^12) =
2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10)/(64*10^12)
* Scenario q9; the chance that one of the children of second gen and only his partners have (AB):
[(100x^3-x^4)/80000][(80000-100x^3-x^4)/80000]*[(100x-x^2)/5000] =
[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[(100x-x^2)/5000] =
(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(100x-x^2)/(32*10^12) =
2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
* Scenario q10; the chance that one of the children of second gen and only the partner of the other child of the 2nd gen have (AB):
[(100x^3-x^4)/80000][(80000-100x^3-x^4)/80000]*[(100x-x^2)/5000] =
[(100x^3-x^4)(80000-100x^3-x^4)/(64*10^8)]*[(100x-x^2)/5000] =
(8*10^6x^3 -8*10^4x^4 -10^4x^6 +x^8)(100x-x^2)/(32*10^12) =
2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
Third generation:
* Chance that a child from the 3th gen has (AB):
[q1/2 + (q2/2 + q2/4)/2 + q3/4 + q4/4 + (q5*0 + q5/4)/2 + q6*0 + (q7/2 + q7/4)/2 + (q8*0 +q8/4)/2 + (q9*0 + q9/2)/2 + q10/4]/10 =
(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)/10
* Scenario r; the chance that both cousins from the 3th gen have (AB):
[(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)/10]^2
(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)^2/100
Fourth generation:
* Chance that the child from our two cousins is born with a genetic defect (BB):
f(x) = r/4
f(x) = [(q1/2 + 3q2/8 + q3/4 + q4/4 + q5/8 + 3q7/8 + q8/8 + q9/4 + q10/4)^2/100]/4
f(x) = (4q1/8 + 3q2/8 + 2q3/8 + 2q4/8 + q5/8 + 3q7/8 + q8/8 + 2q9/8 + 2q10/8)^2/400
f(x) = [(4q1 +3q2 +2q3 +2q4 +q5 +3q7 +q8 +2q9 +2q10)/8]^2/400
f(x) = (4q1 +3q2 +2q3 +2q4 +q5 +3q7 +q8 +2q9 +2q10)^2/256*10^2
If we now fill in the values:
q1 = (10^4x^8-200x^9+x^6)/(64*10^12)
q2 = (100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9)/(64*10^12)
q3 = (10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7+ 4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6)/(64*10^12)
q4 = (64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10)/(64*10^12)
q5 = 4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10)/(64*10^12)
q7 = 2[(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10)/(64*10^12)
q8 = 2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10)/(64*10^12)
q9 = 2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
q10 = 2(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)
We get:
f(x) = [4(10^4x^8-200x^9+x^6)/(64*10^12) +3(100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9)/(64*10^12) +2(10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7+ 4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6)/(64*10^12) +2(64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10)/(64*10^12) +4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10)/(64*10^12) +6(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10)/(64*10^12) +2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10)/(64*10^12) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)/(64*10^12)]^2/256*10^2
Adding up the fractions:
f(x) = [[4(10^4x^8-200x^9+x^6) +3(100x^5 -x^6 +10^6x^7 -3*10^4x^8 +200x^9) +2(10^8x^6 -2*10^6x^7 +10^4x^4 -2*10^6x^7 +4*10^4x^8 -200x^5 +10^4x^8 -200x^9 +x^6) +2(64*10^8x^2 -16*10^6x^5 -16*10^4x^6 +10^4x^8 +200x^9 +x^10) +4(64*10^10x -64*10^8x^2 -16*10^8x^4 +16*10^4x^6 +10^6x^7 +10^4x^8 -100x^9 -x^10) +6(8*10^6x^5 -8*10^4x^6 -10^4x^8 +x^10) +2(8*10^10x^3 -16*10^8x^4 +16*10^6x^5 -10008*10^4x^6 +10^6x^7 -10^2x^9 +x^10) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10) +4(8*10^8x^4 -16*10^6x^5 +8*10^4x^6 -10^6x^7 +10^4x^8 +10^2x^9 -x^10)]^2/(64*10^12)^2]/256*10^2
Working out the numberator:
f(x) =[(4*10^4x^8-8*10^2x^9+4x^6 +3*10^2x^5 -3x^6 +3*10^6x^7 -9*10^4x^8 +6*10^2x^9 +2*10^8x^6 -4*10^6x^7 +2*10^4x^4 -4*10^6x^7 +8*10^4x^8 -400x^5 +2*10^4x^8 -400x^9 +2x^6 +128*10^8x^2 -32*10^6x^5 -32*10^4x^6 +2*10^4x^8 +400x^9 +2x^10 +256*10^10x -256*10^8x^2 -64*10^8x^4 +64*10^4x^6 +4*10^6x^7 +4*10^4x^8 -400x^9 -4x^10 +48*10^6x^5 -48*10^4x^6 -6*10^4x^8 +6x^10 +16*10^10x^3 -32*10^8x^4 +32*10^6x^5 -20016*10^4x^6 +2*10^6x^7 -2*10^2x^9 +2x^10 +32*10^8x^4 -64*10^6x^5 +32*10^4x^6 -4*10^6x^7 +4*10^4x^8 +4*10^2x^9 -4x^10 +32*10^8x^4 -64*10^6x^5 +32*10^4x^6 -4*10^6x^7 +4*10^4x^8 +4*10^2x^9 -4x^10)^2/(4.096*10^27)]/256*10^2
Adding up:
f(x) = (+256*10^10x -128*10^8x^2 +16*10^10x^3 -320002*10^4x^4 -800001*10^2x^5 +320003x^6 -7*10^6x^7 +13*10^4x^8 -2x^10)^2/(1.048576*10^32)
* The chance of two unrelated people having a child with trait (BB)
g(x) = [(x/100)^2]/4
g(x) = x^2/40000
Last edited: