You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematics Corner :)
- Thread starter Ameeratul Layl
- Start date
- Replies 399
- Views 42K
British Wholesales - Certified Wholesale Linen & Towels | Halal Food Gastronomy | PHP 8.4 patch for vBulletin 4.2.5
Banu_Hashim
A slave of Allaah
- Messages
- 1,704
- Reaction score
- 259
- Gender
- Male
- Religion
- Islam
Is this C4?
Musaafirah
Miss. Serious ^_^
- Messages
- 1,979
- Reaction score
- 282
- Gender
- Female
- Religion
- Islam
I believe they start calculus your third or fourth(the last) year in high school. So I'd say mainly 16/17/18 ish. On that note, I'm surprised you started at 14/15!
It really depends though which math track you're on. Some people are quite blessed, they go on a faster track. Others don't touch a real calculus until they've graduate their fourth year in high school and gone to a university.
You're saying the final years of high school right? Years 10/11 are our final years, though I covered calculus in more detail when I studied for A-level Maths.
And promptly forgot everything.
- Messages
- 7,146
- Reaction score
- 843
- Gender
- Female
- Religion
- Islam
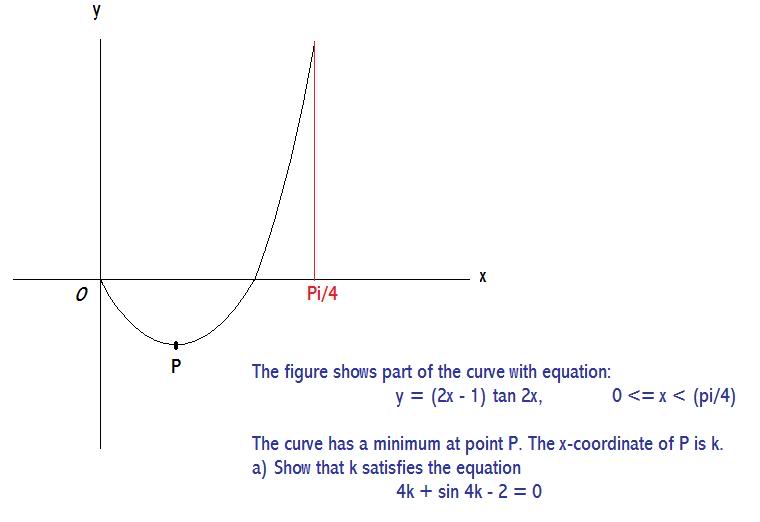
I think I did a fantastic job with Paint. I'm rather proud of what I've done. Anyway... I have no clue where to start or what to do.
And I just noticed that the actual question seems to have an 'O' instead of 'y' in the y-axis. So, I suppose, it's an O-axis now.
~Raynn~
Esteemed Member
- Messages
- 205
- Reaction score
- 28
Lol, wow, that IS a pretty amazing graph...
Okayy, you start by finding dy/dx; use the product rule...you get:
dy/dx = 2tan2x + (2x-1)(2sec^2(2x)) = 2tan2x + 4xsec^2(2x) - 2sec^2(2x)
At the stationary point P, x = k, and dy/dx = 0, so set the above expression ^^ to equal zero, and replace x with k:
2tan2k + 4xsec^2(2k) - 2sec^2(2k) = 0
Multiply throughout by cos^2(2k) - or divide by sec^2(2k) - to get:
2(cos^2(2k))(tan2k) + 4k - 2 = 0
2(cos2k)(sin2k) + 4k - 2 = 0 .......[because cosxtanx = sinx, so cos^2xtanx = cosxsinx]
sin4k + 4k - 2 = 0 ........[double angle formula for sinx]
Therefore 4k + sin4k - 2 = 0
Okayy, you start by finding dy/dx; use the product rule...you get:
dy/dx = 2tan2x + (2x-1)(2sec^2(2x)) = 2tan2x + 4xsec^2(2x) - 2sec^2(2x)
At the stationary point P, x = k, and dy/dx = 0, so set the above expression ^^ to equal zero, and replace x with k:
2tan2k + 4xsec^2(2k) - 2sec^2(2k) = 0
Multiply throughout by cos^2(2k) - or divide by sec^2(2k) - to get:
2(cos^2(2k))(tan2k) + 4k - 2 = 0
2(cos2k)(sin2k) + 4k - 2 = 0 .......[because cosxtanx = sinx, so cos^2xtanx = cosxsinx]
sin4k + 4k - 2 = 0 ........[double angle formula for sinx]
Therefore 4k + sin4k - 2 = 0
Whatsthepoint
Account Disabled
- Messages
- 3,705
- Reaction score
- 367
x satisfies this equation
cos(2x) + cos(3x) = 1
Show that it also satisfies this one:
2sin(2x) + 2sin(3x) = sin(4x) + 2sin(5x) + sin(6x)
hEr's one for ya, Raynn
cos(2x) + cos(3x) = 1
Show that it also satisfies this one:
2sin(2x) + 2sin(3x) = sin(4x) + 2sin(5x) + sin(6x)
hEr's one for ya, Raynn
~Raynn~
Esteemed Member
- Messages
- 205
- Reaction score
- 28
Difficult stuff indeed. But maybe that's because I'm mesmerised by my art to focus on the differentiation. I think I'll take a break and then come back.
Lol, yup, good idea...using the product rule gets wayy complicated in this example...
x satisfies this equation
cos(2x) + cos(3x) = 1
Show that it also satisfies this one:
2sin(2x) + 2sin(3x) = sin(4x) + 2sin(5x) + sin(6x)
hEr's one for ya, Raynn
Lol, it looked like this was gonna take foreverr, but it wasn't too bad...so, we're trying to show:
2sin(2x) + 2sin(3x) = sin(4x) + 2sin(5x) + sin(6x)
Starting with the right side, and used the double angle formula for sinx,
sin4x + 2sin5x + sin6x
= 2sin2xcos2x + 2(sin2xcos3x + sin3xcos2x) + 2sin3xcos3x ......[the only odd angle is the sin5x; divide that into 2x and 3x]
= (2sin2xcos2x + 2sin2xcos3x) + (2sin3xcos2x + 2sin3xcos3x).....[regrouping]
= 2sin2x(cos2x + cos3x) + 2sin3x(cos2x + cos3x)......[factorizing]
We know from the previous identity thing that (cos2x + cos3x) = 1
Therefore,
sin4x + 2sin5x + sin6x = 2sin2x(1) + 2sin3x{1)
sin4x + 2sin5x + sin6x = 2sin2x + 2sin3x
There we are!
Last edited:
Whatsthepoint
Account Disabled
- Messages
- 3,705
- Reaction score
- 367
Yep.Lol, yup, good idea...using the product rule gets wayy complicated in this example...
Lol, it looked like this was gonna take foreverr, but it wasn't too bad...so, we're trying to show:
2sin(2x) + 2sin(3x) = sin(4x) + 2sin(5x) + sin(6x)
Starting with the right side, and used the double angle formula for sinx,
sin4x + 2sin5x + sin6x
= 2sin2xcos2x + 2(sin2xcos3x + sin3xcos2x) + 2sin3xcos3x ......[the only odd angle is the sin5x; divide that into 2x and 3x]
= (2sin2xcos2x + 2sin2xcos3x) + (2sin3xcos2x + 2sin3xcos3x).....[regrouping]
= 2sin2x(cos2x + cos3x) + 2sin3x(cos2x + cos3x)......[factorizing]
We know from the previous identity thing that (cos2x + cos3x) = 1
Therefore,
sin4x + 2sin5x + sin6x = 2sin2x(1) + 2sin3x{1)
sin4x + 2sin5x + sin6x = 2sin2x + 2sin3x
There we are!
when I was supposed to know it I didn't know all these formulas, like sin (alpha + beta).
You're officially an aspie, Raynn.:skeleton:
- Messages
- 7,146
- Reaction score
- 843
- Gender
- Female
- Religion
- Islam
2(cos2k)(sin2k) + 4k - 2 = 0 .......[because cosxtanx = sinx, so cos^2xtanx = cosxsinx]
sin4k + 4k - 2 = 0 ........[double angle formula for sinx]
Therefore 4k + sin4k - 2 = 0
Those are the bits I'm having difficulty understanding. Are those just formulae I'm supposed to know?
- Messages
- 7,146
- Reaction score
- 843
- Gender
- Female
- Religion
- Islam
a) sin^2 x + cos^2 x = 1, show that cosec^2 x - cot^2 x = 1
I could do that.
b) Hence, or otherwise, prove that
cosec^4 x - cot^4 x = cosec^2 x + cot^2 x
... And I'm stuck. It's only for 2 marks so I think I'm missing something obvious here.
It's a proof, by the way.
I could do that.
b) Hence, or otherwise, prove that
cosec^4 x - cot^4 x = cosec^2 x + cot^2 x
... And I'm stuck. It's only for 2 marks so I think I'm missing something obvious here.
It's a proof, by the way.
Last edited:
- Messages
- 7,146
- Reaction score
- 843
- Gender
- Female
- Religion
- Islam
Done?
you mean you found the mistake
By done I meant I edited the post. *sweatdrops*
I still can't figure out what I'm doing wrong.
Similar Threads
Add to Homescreen
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
